|
Problema Dato un qualunque triangolo isoscele e considerata la circonferenza in esso inscritta, dimostrare che la distanza della base dal punto di contatto della circonferenza con ognuno dei lati congruenti e' la meta' della misura dell'altezza relativa ad ognuno dei lati congruenti Per risolvere il problema occorre sapere che i segmenti di tangente condotti da un punto esterno ad una circonferenza sono sempre congruenti, ancora non l'abbiamo fatto, quindi te lo anticipo, ma che ne dici di provare a dimostrarlo? Qui il difficile e' capire il testo e fare bene la figura: una volta fatta bene la figura il problema diventa elementare; nella figura per semplicita' considero uno dei lati congruenti per volta, poi posso ripetere il ragionamemto per l'altro ED e' la distanza dalla base del punto di contatto della circonferenza con il lato AB BH e' l'altezza relativa al lato AH 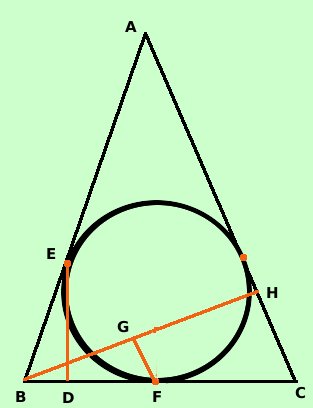
Considero i triangoli BED e BHC, essi hanno: EBD = BCH^ ^perche' angoli alla base di un triangolo isoscele BDE = BHC^ ^perche' angoli retti (per ipotesi) Quindi per il primo criterio di similitudine i due triangoli BED e BHC sono simili. Costruisco il triangolo BFG mandando dal punto di tangenza F della circonferenza con la base la perpendicolare alla retta BH sino ad incontrarla in G. Considero ora i triangoli BFG e BCH, essi hanno: L'angolo CBH^ in comune BGF = BHC^ ^perche' angoli retti Ne deriva che le rette FG ed HC sono parallele (avendo gli angoli corrispondenti rispetto alla trasversale BH congruenti) ed essendo BC = 2BF segue BH = 2BG (esercizio sul corollario del teorema di Talete) Dimostriamo infine che i triangoli BDE e BFG sono congruenti Infatti tali triangoli hanno: gli angoli ordinatamente uguali perche' sono simili (infatti BDE e' simile a BHC e quest'ultimo e' simile a BFG, quindi, per la proprieta' transitiva della similitudine i due triangoli sono simili e quindi hanno tutti gli angoli congruenti BE = BF perche' segmenti di tangente condotti da un punto esterno ad una circonferenza (fare link quando sara' fatto) Quindi per il secondo criterio di congruenza, avendo due angoli ed il lato compreso congruenti i due triangoli sono congruenti, in particolare ED = BG ed essendo BH = 2BG ne segue BH = 2ED come volevamo |